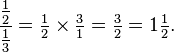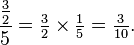Addition
The first rule of addition is that only like quantities can be added; for example, various quantities of quarters. Unlike quantities, such as adding thirds to quarters, must first be converted to like quantities as described below: Imagine a pocket containing two quarters, and another pocket containing three quarters; in total, there are five quarters. Since four quarters is equivalent to one (dollar), this can be represented as follows: .
.
Adding unlike quantities
To add fractions containing unlike quantities (e.g. quarters and thirds), it is necessary to convert all amounts to like quantities. It is easy to work out the chosen type of fraction to convert to; simply multiply together the two denominators (bottom number) of each fraction.For adding quarters to thirds, both types of fraction are converted to
 (twelfths).
(twelfths).Consider adding the following two quantities:
 into twelfths by multiplying both the numerator and denominator by three:
into twelfths by multiplying both the numerator and denominator by three:  . Note that
. Note that  is equivalent to 1, which shows that
is equivalent to 1, which shows that  is equivalent to the resulting
is equivalent to the resulting  .
.Secondly, convert
 into twelfths by multiplying both the numerator and denominator by four:
into twelfths by multiplying both the numerator and denominator by four:  . Note that
. Note that  is equivalent to 1, which shows that
is equivalent to 1, which shows that  is equivalent to the resulting
is equivalent to the resulting  .
.Now it can be seen that:
 and
and  the denominator 48 can be used (the product of 4 and 12), but the smaller denominator 12 may also be used, being the least common multiple of 4 and 12.
the denominator 48 can be used (the product of 4 and 12), but the smaller denominator 12 may also be used, being the least common multiple of 4 and 12.Subtraction
The process for subtracting fractions is, in essence, the same as that of adding them: find a common denominator, and change each fraction to an equivalent fraction with the chosen common denominator. The resulting fraction will have that denominator, and its numerator will be the result of subtracting the numerators of the original fractions. For instance,Comparing fractions
Comparing fractions with the same denominator only requires comparing the numerators. because 3>2.
because 3>2.
One way to compare fractions with different numerators and denominators is to find a common denominator. To compare
 and
and  , these are converted to
, these are converted to  and
and  . Then bd is a common denominator and the numerators ad and bc can be compared.
. Then bd is a common denominator and the numerators ad and bc can be compared.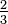 ?
?  gives
gives 
 ?
? 
 ?
? 
 .
.Also note that every negative number, including negative fractions, is less than zero, and every positive number, including positive fractions, is greater than zero, so every negative fraction is less than any positive fraction.
Equivalent fractions
Multiplying the numerator and denominator of a fraction by the same (non-zero) number results in a fraction that is equivalent to the original fraction. This is true because for any non-zero number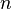 , the fraction
, the fraction  . Therefore, multiplying by
. Therefore, multiplying by  is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction
is equivalent to multiplying by one, and any number multiplied by one
has the same value as the original number. By way of an example, start
with the fraction  . When the numerator and denominator are both multiplied by 2, the result is
. When the numerator and denominator are both multiplied by 2, the result is  , which has the same value (0.5) as
, which has the same value (0.5) as  . To picture this visually, imagine cutting a cake into four pieces; two of the pieces together (
. To picture this visually, imagine cutting a cake into four pieces; two of the pieces together ( ) make up half the cake (
) make up half the cake ( ).
).Dividing the numerator and denominator of a fraction by the same non-zero number will also yield an equivalent fraction. This is called reducing or simplifying the fraction. A simple fraction in which the numerator and denominator are coprime [that is, the only positive integer that goes into both the numerator and denominator evenly is 1) is said to be irreducible, in lowest terms, or in simplest terms. For example,
 is not in lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,
is not in lowest terms because both 3 and 9 can be exactly divided by 3. In contrast,  is in lowest terms—the only positive integer that goes into both 3 and 8 evenly is 1.
is in lowest terms—the only positive integer that goes into both 3 and 8 evenly is 1.Using these rules, we can show that
 =
=  =
=  =
=  .
.A common fraction can be reduced to lowest terms by dividing both the numerator and denominator by their greatest common divisor. For example, as the greatest common divisor of 63 and 462 is 21, the fraction
 can be reduced to lowest terms by dividing the numerator and denominator by 21:
can be reduced to lowest terms by dividing the numerator and denominator by 21:Reciprocals and the "invisible denominator"
The reciprocal of a fraction is another fraction with the numerator and denominator reversed. The reciprocal of , for instance, is
, for instance, is 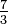 . The product of a fraction and its reciprocal is 1, hence the reciprocal is the multiplicative inverse of a fraction. Any integer can be written as a fraction with the number one as denominator. For example, 17 can be written as
. The product of a fraction and its reciprocal is 1, hence the reciprocal is the multiplicative inverse of a fraction. Any integer can be written as a fraction with the number one as denominator. For example, 17 can be written as  , where 1 is sometimes referred to as the invisible denominator. Therefore, every fraction or integer except for zero has a reciprocal. The reciprocal of 17 is
, where 1 is sometimes referred to as the invisible denominator. Therefore, every fraction or integer except for zero has a reciprocal. The reciprocal of 17 is  .
.Complex fractions
In a complex fraction, either the numerator, or the denominator, or both, is a fraction or a mixed number[8][9], corresponding to division of fractions. For example,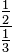 and
and  are complex fractions. To reduce a complex fraction to a simple
fraction, treat the longest fraction line as representing division. For
example:
are complex fractions. To reduce a complex fraction to a simple
fraction, treat the longest fraction line as representing division. For
example:Compound fractions
A compound fraction is a fraction of a fraction, or any number of fractions connected with the word of[8][9], corresponding to multiplication of fractions. To reduce a compound fraction to a simple fraction, just carry out the multiplication (see the section on multiplication). For example, of
of  is a compound fraction, corresponding to
is a compound fraction, corresponding to  . The terms compound fraction and complex fraction are closely related and sometimes one is used as a synonym for the other.
. The terms compound fraction and complex fraction are closely related and sometimes one is used as a synonym for the other.Decimal fractions and percentages
A decimal fraction is a fraction whose denominator is not given explicitly, but is understood to be an integer power of ten. Decimal fractions are commonly expressed using decimal notation in which the implied denominator is determined by the number of digits to the right of a decimal separator, the appearance of which (e.g., a period, a raised period (•), a comma) depends on the locale (for examples, see decimal separator). Thus for 0.75 the numerator is 75 and the implied denominator is 10 to the second power, viz. 100, because there are two digits to the right of the decimal separator. In decimal numbers greater than 1 (such as 3.75), the fractional part of the number is expressed by the digits to the right of the decimal (with a value of 0.75 in this case). 3.75 can be written either as an improper fraction, 375/100, or as a mixed number, .
.Decimal fractions can also be expressed using scientific notation with negative exponents, such as 6.023×10−7, which represents 0.0000006023. The 10−7 represents a denominator of 107. Dividing by 107 moves the decimal point 7 places to the left.
Decimal fractions with infinitely many digits to the right of the decimal separator represent an infinite series. For example, 1/3 = 0.333... represents the infinite series 3/10 + 3/100 + 3/1000 + ... .
Another kind of fraction is the percentage (Latin per centum meaning "per hundred", represented by the symbol %), in which the implied denominator is always 100. Thus, 75% means 75/100. Related concepts are the permille, with 1000 as implied denominator, and the more general parts-per notation, as in 75 parts per million, meaning that the proportion is 75/1,000,000.
Whether common fractions or decimal fractions are used is often a matter of taste and context. Common fractions are used most often when the denominator is relatively small. By mental calculation, it is easier to multiply 16 by 3/16 than to do the same calculation using the fraction's decimal equivalent (0.1875). And it is more accurate to multiply 15 by 1/3, for example, than it is to multiply 15 by any decimal approximation of one third. Monetary values are commonly expressed as decimal fractions, for example $3.75. However, as noted above, in pre-decimal British currency, shillings and pence were often given the form (but not the meaning) of a fraction, as, for example 3/6 (read "three and six") meaning 3 shillings and 6 pence, and having no relationship to the fraction 3/6.
Special cases
- A unit fraction is a vulgar fraction with a numerator of 1, e.g.
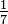 . Unit fractions can also be expressed using negative exponents, as in 2−1 which represents 1/2, and 2−2 which represents 1/(22) or 1/4.
. Unit fractions can also be expressed using negative exponents, as in 2−1 which represents 1/2, and 2−2 which represents 1/(22) or 1/4.
- An Egyptian fraction is the sum of distinct positive unit fractions, for example
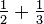 . This definition derives from the fact that the ancient Egyptians expressed all fractions except
. This definition derives from the fact that the ancient Egyptians expressed all fractions except  ,
, 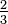 and
and  in this manner. Every positive rational number can be expanded as an Egyptian fraction. For example,
in this manner. Every positive rational number can be expanded as an Egyptian fraction. For example,  can be written as
can be written as  Any positive rational number can be written as a sum of unit fractions in infinitely many ways. Two ways to write
Any positive rational number can be written as a sum of unit fractions in infinitely many ways. Two ways to write  are
are  and
and  .
.
- A dyadic fraction is a vulgar fraction in which the denominator is a power of two, e.g.
 .
.
Mixed numbers
A mixed numeral (often called a mixed number, also called a mixed fraction) is the sum of a non-zero integer and a proper fraction. This sum is implied without the use of any visible operator such as "+". For example, in referring to two entire cakes and three quarters of another cake, the whole and fractional parts of the number are written next to each other: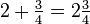 .
.This is not to be confused with the algebra rule of implied multiplication. When two algebraic expressions are written next to each other, the operation of multiplication is said to be "understood". In algebra,
 for example is not a mixed number. Instead, multiplication is understood:
for example is not a mixed number. Instead, multiplication is understood:  .
.An improper fraction is another way to write a whole plus a part. A mixed number can be converted to an improper fraction as follows:
- Write the mixed number
 as a sum
as a sum 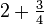 .
. - Convert the whole number to an improper fraction with the same denominator as the fractional part,
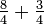 .
. - Add the fractions. The resulting sum is the improper fraction. In the example,
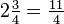 .
.
- Divide the numerator by the denominator. In the example,
 , divide 11 by 4. 11 ÷ 4 = 2 with remainder 3.
, divide 11 by 4. 11 ÷ 4 = 2 with remainder 3. - The quotient (without the remainder) becomes the whole number part of the mixed number. The remainder becomes the numerator of the fractional part. In the example, 2 is the whole number part and 3 is the numerator of the fractional part.
- The new denominator is the same as the denominator of the improper fraction. In the example, they are both 4. Thus
 .
.
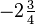 , which equals
, which equals  .
.Proper and improper common fractions
Common fractions can be classified as either proper or improper. When the numerator and the denominator are both positive, the fraction is called proper if the numerator is less than the denominator, and improper otherwise.[4][5] In general, a common fraction is said to be a proper fraction if the absolute value of the fraction is strictly less than one—that is, if the fraction is between -1 and 1 (but not equal to -1 or 1).[6][7] It is said to be an improper fraction (U.S., British or Australian) or top-heavy fraction (British, occasionally North America) if the absolute value of the fraction is greater than or equal to 1. Examples of proper fractions are 2/3, -3/4, and 4/9; examples of improper fractions are 9/4, -4/3, and 8/3.Fraction
A common or vulgar fraction, such as 1/2, 8/5, 3/4, consists of an integer numerator and a non-zero integer denominator—the numerator representing a number of equal parts and the denominator indicating how many of those parts make up a whole. An example is A cake with one quarter removed. The remaining three quarters are shown. Dotted lines indicate where the cake may be cut in order to divide it into equal parts. Each quarter of the cake is denoted by the fraction 1/4.3/4, in which the numerator, 3, tells us that the fraction represents 3 equal parts, and the denominator, 4, tells us that 4 parts equal a whole. The picture to the right illustrates 3/4 of a cake.
Fractional numbers can also be written without using explicit numerators or denominators, by using decimals, percent signs, or negative exponents (as in 0.01, 1%, and 10−2 respectively, all of which are equivalent to 1/100). An integer such as the number 7 can be thought of as having an implied denominator of one: 7 equals 7/1.
Other uses for fractions are to represent ratios and to represent division.[1] Thus the fraction 3/4 is also used to represent the ratio 3:4 (the ratio of the part to the whole) and the division 3 ÷ 4 (three divided by four).
In mathematics the set of all numbers which can be expressed in the form a/b, where a and b are integers and b is not zero, is called the set of rational numbers and is represented by the symbol Q, which stands for quotient. The test for a number being a rational number is that it can be written in that form (i.e., as a common fraction). However, the word fraction is also used to describe mathematical expressions that are not rational numbers, for example algebraic fractions (quotients of algebraic expressions), and expressions that contain irrational numbers, such as √2/2 (see square root of 2) and π/4 (see proof that π is irrational).
Division games & exercises
Maths division is hard. It's OK to admit it. We won't make you a division genius overnight, but we will help you with halving, times tables, factors, remainders, speed questions, and even dreaded long division!Click below to start playing.
http://www.whizz.com/maths/division/games/
http://www.eduplace.com/kids/mthexp/g4/index.html


 of a cake is to be added to
of a cake is to be added to  of a cake, the pieces need to be converted into comparable quantities, such as cake-eighths or cake-quarters.
of a cake, the pieces need to be converted into comparable quantities, such as cake-eighths or cake-quarters.